I’m the first to admit that the Word Judge is booooring application. Checking if the word can be used in a word game? Meh. From a programmer perspective however, there is one very interesting problem to solve – how to compress a large dictionary to reduce the size of the application package and at the same time be able to query this dictionary without using excessive amount of memory and CPU power?

First, let’s settle on what is a “large dictionary”. One of the languages supported by Word Judge is Polish, for which the valid word list has over 2 million entries and takes about 36MB after unpacking. Do we need to compress this data at all? Probably not. If you consider the average hardware spec and modern network speed, the 36MB is not much, but we can do so much better. Besides, it’s fun!

One the other end of the spectrum is the “zip all the things” approach. It’s not a good idea though – it puts a very heavy load on the CPU and doesn’t compress the data that well. The zipped Polish dictionary takes 4.5MB.

The most important observation is that we’re not compressing some random white noise, but words from real language. We can leverage this information to get a much better compression than some generic algorithm. Lot of words share the same prefix and suffix, which means they can be efficiently represented as a directed acyclic graph with shared nodes for common prefixes and suffixes. Let’s see how the graph would look like for couple of words:

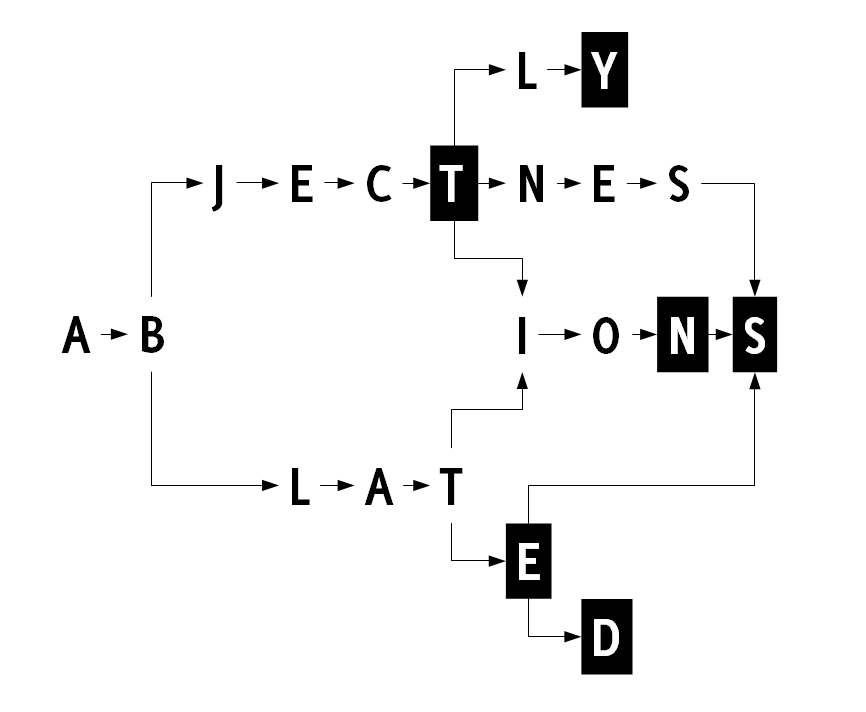
White letters on black background mark the nodes representing the ends of words. So the graph above represents the following words:

1
2
3
4
5
6
7
8
9

abject
abjection
abjections
abjectly
abjectness
ablate
ablated
ablation
ablations

The nodes for ab prefix are of course shared, the ions, s suffixes nodes as well. For obvious reasons we cannot share the t node: in one group it marks the end of the word, in other it does not; the child nodes for each ’t’ nodes are also different. Nodes are equal, and thus can be shared, if and only if they represent the same letter, the End Of Word flag is the same for both of them, and the list of children is exactly the same.

This type of graph contains minimal number of nodes, but each node takes quite a lot of space. We need 8 bits for the letter, 1 bit for EOW flag, 8 bits for the children list length and some kind of reference, for example node index, to each child, which is log2(n) rounded up bits, where n is a number of nodes in the graph. As you can see the major contributor to a single node size is the children list: for TWL06 dictionary the number of nodes is in the 10k-100k order of magnitude, which means we need several bits per node index.

A guy called John Paul Adamovsky found a neat solution to that. Instead of keeping the full list of children, we can keep children in something similar to singly-linked list: let’s store only the index of the first child, number the nodes in such way that the children always have consecutive indices and add a End Of Children List flag to each node. This way we need exactly 1 + log2(n) bits for child list. This way we can keep the entire node in one byte. What’s the catch? We need to introduce few more nodes.

For example on the graph above we can no longer share the i node in the ions suffix: if it was shared it would have to have a number one greater than the number of both e node in ablate and n node in abjectness (this is, of course, assuming the i node is the last on the child list of both t nodes; but it’s impossible for any node ordering). Our graph would look like this:

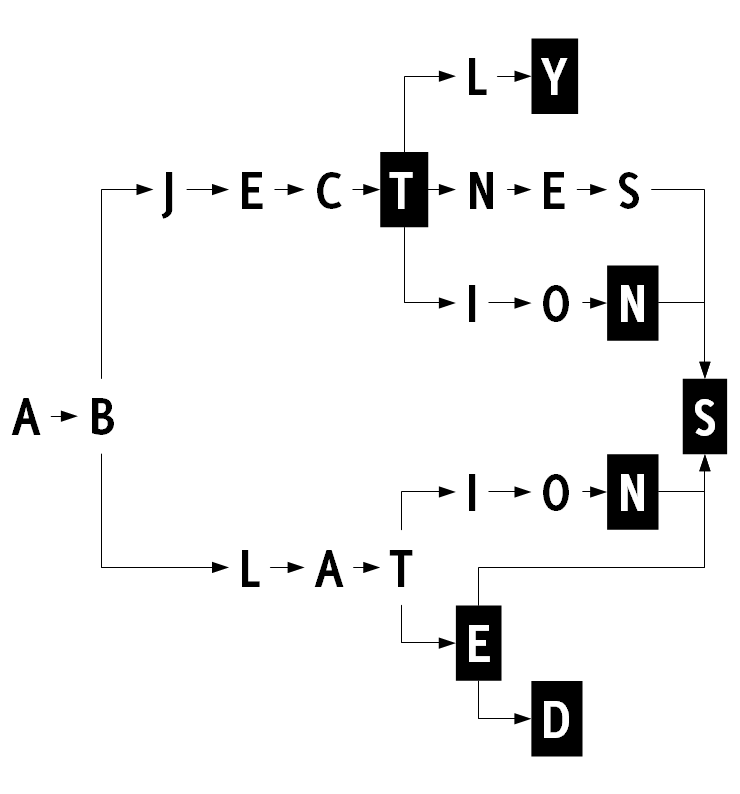
The rule for node equality has to be extended: the nodes are equal if they represent the same letter, the flags are the same, the children are equal and the siblings further on the children list are equal. The last condition is a bit confusing, so I’ll provide an example.

Let’s add a absolution and absolutions to our dictionary. We can certainly share the ab prefix and ons suffix, but do we need a separate i node as well? The i node in absolution must have a End-Of-Child-List flag set. If we arrange the child nodes in either ablat- or abject- part of graph in such way that the i node is the last node, we can share the i node between that part of graph and the newly added branch. Our graph would look like this:

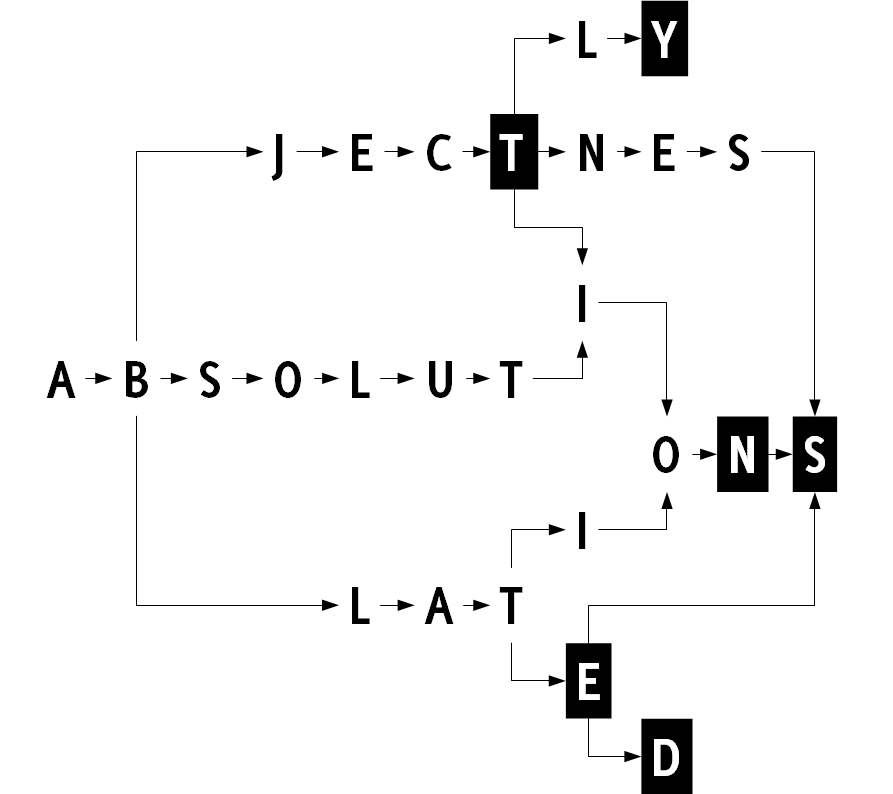
This is the way we can squeeze the 36MB dictionary to 1.5MB. The structure also doesn’t need any processing, it can be loaded to int array and used directly. If you’re curious how to convert the dictionary into this kind of graph you can read the description of my dawggenerator project on github (C++) or the original description by John Paul Adamovsky (pure C).